Have you ever thought that SQL can be wrong in math? It sounds crazy. But if you’ve used the SQL FLOAT data type, you may have come across the problems I am about to show you.
Consider this. 0.1 + 0.2 should be 0.3, right? But check this out using SQL FLOAT data type.
DECLARE @f1 FLOAT = 0.1
DECLARE @f2 FLOAT = 0.2
SELECT CASE WHEN @f1 + @f2 = .3 THEN 1 ELSE 0 END
The correct result is 1. But check Figure 1.
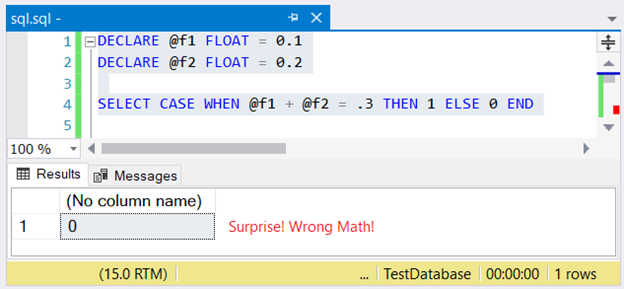
Do I have your attention now? I sure hope so. It’s quite scary to depend on a system that won’t give us correct math. But this article will help you avoid this.
There’s some work to do. We need to start from what a FLOAT data type is all about.
What is SQL FLOAT Data Type?
SQL FLOAT data type is an approximate numeric data type used for floating-point numbers. They can store very large or very small numbers. They are also used for computations that require fast processing times.
All these come at the cost of the loss of precision. Further, you can’t say where the decimal point will be placed after the computation – it floats. Meanwhile, exact numerics like DECIMAL will have a fixed decimal point position.
How You Declare an SQL FLOAT Data Type
The syntax is FLOAT[(n)], where n is the number of bits used to store the mantissa of a floating-point number in scientific notation. That also dictates the precision and storage size. The possible values for n are between 1 to 53. Note that n is optional.
Here’s an example:
DECLARE @floatValue1 FLOAT; -- Float variable without the number of bits
DECLARE @floatValue2 FLOAT(3) -- Float variable with 3 bits
If you do not specify n, the default is 53. That is also the maximum value. Further, FLOAT(53) is a double-precision floating-point number or binary64. Aside from using FLOAT(53), you can also declare it as DOUBLE PRECISION.
The following 3 declarations are functionally equivalent:
DECLARE @double1 FLOAT(53);
DECLARE @double2 FLOAT;
DECLARE @double3 DOUBLE PRECISION;
The table shows the number of bits and the corresponding storage size.
| Value of n | Storage Size |
| 1 to 24 | 4 bytes |
| 25 to 53 | 8 bytes |
Is SQL FLOAT and REAL the Same?
REAL is also FLOAT(24). It is also referred to as single-precision or binary32.
Why Knowing This is Important
Knowing that this is an approximate numeric will stop you from using it for calculations that require accuracy. Are you also concerned with storage and memory? Use REAL or FLOAT(24) if you don’t need too large or too small values.
What are the Differences Between FLOAT and DECIMAL?
FLOAT is an approximate numeric. DECIMAL is an exact numeric. Here’s a summary of the differences in a Table:
| FLOAT | DECIMAL | |
| Decimal Point | Can be placed anywhere in the digit | Fixed position |
| Maximum Limit | 38 digits or 99,999,999,999,999,999,999,999,999,999,999,999,999 | FLOAT(53) has a maximum range of 1.79E+308 or 179 followed by 306 zeroes |
| Storage | Maximum of 8 bytes | Maximum of 17 bytes |
| Computational Result | Approximate | Exact |
| Comparison checks | Do not use = or <>. Avoid when rounding off | = or <> operators. Good for rounding off |
You already saw in Figure 1 how computing a FLOAT number can have weird results. If you change the data type to DECIMAL like this:
DECLARE @d1 DECIMAL(2,1) = 0.1
DECLARE @d2 DECIMAL(2,1) = 0.2
SELECT CASE WHEN @d1 + @d2 = 0.3 THEN 1 ELSE 0 END
The result will be correct.
Using an inequality operator is also a problem. Check out the loop below.
DECLARE @floatValue FLOAT(1) = 0.0
WHILE @floatValue <> 5.0
BEGIN
PRINT @floatValue;
SET @floatValue += 0.1;
END
What do you think? See Figure 2 below.
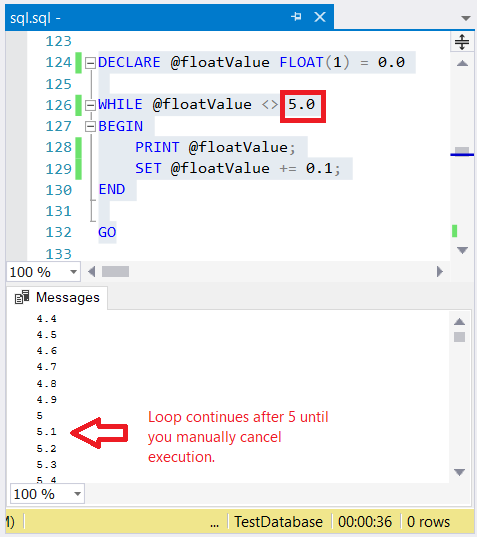
Boom! Infinite loop! The inequality condition will always be true. So, the logical choice is to change the type to DECIMAL.
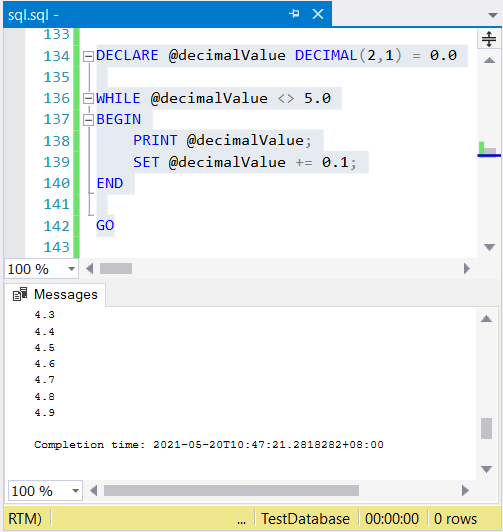
DECLARE @decimalValue DECIMAL(2,1) = 0.0
WHILE @decimalValue <> 5.0
BEGIN
PRINT @decimalValue;
SET @decimalValue += 0.1;
END
The above code will surely stop when @decimalValue is equal to 5.0. See for yourself in Figure 3 below.
Nice! But if you still insist on FLOAT, this will work just fine without the infinite loop.
DECLARE @floatValue FLOAT(1) = 0.0
WHILE @floatValue < 5.0
BEGIN
PRINT @floatValue;
SET @floatValue += 0.1;
END
Meanwhile, rounding off is also off. Consider the following:
DECLARE @value FLOAT(2) = 1.15
SELECT ROUND(@value, 1) -- This will result to 1.1
Instead of 1.20, the code results to 1.1. But if you use DECIMAL, the result will be correct.
DECLARE @value DECIMAL(3,2) = 1.15
SELECT ROUND(@value, 1) -- This will result in 1.2 or 1.20
When FLOAT is Correct, and DECIMAL is Not
Are exact numerics NOT so exact all the time? To reproduce this problem, we will use a calculation, and then we reverse it. First, let’s have the data prepared.
CREATE TABLE ExactNumerics1
(
fixed1 DECIMAL(8,4),
fixed2 DECIMAL(8,4),
fixed3 DECIMAL(8,4),
calcValue1 AS fixed3 / fixed1 * fixed2
)
GO
INSERT INTO ExactNumerics1
(fixed1,fixed2,fixed3)
VALUES
(54,0.03,1*54/0.03)
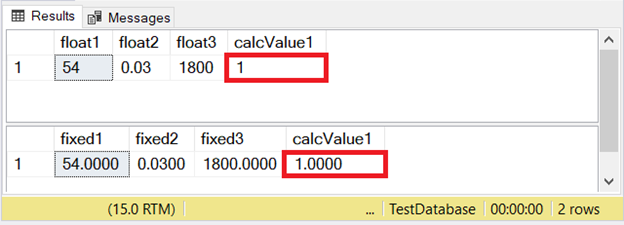
The table above will use fixed values for the first 2 columns. The third column will have the calculation. Finally, the fourth one, which is a computed column, will do the reverse computation. The correct result in the computed column should be 1.
Now, to compare it to FLOAT, let’s create a similar table and data.
CREATE TABLE ApproxNumerics1
(
float1 FLOAT(2),
float2 FLOAT(2),
float3 FLOAT(2),
calcValue1 AS float3 / float1 * float2
)
INSERT INTO ApproxNumerics1
(float1, float2, float3)
VALUES
(54,0.03,1*54/0.03)
Let’s query.
SELECT * FROM ApproxNumerics1
SELECT * FROM ExactNumerics1
The results? Check out Figure 4.
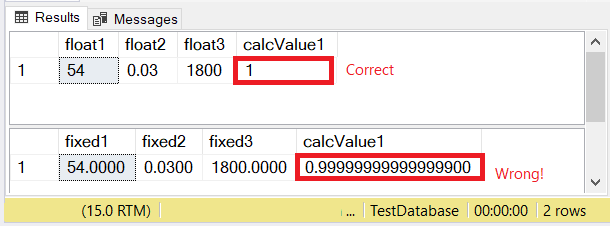
What happened here? FLOAT got it right, but DECIMAL didn’t. Something has gone wrong.
IMPLICIT CONVERSION DOES IT AGAIN
Implicit conversion happens because SQL is forgiving. When different data types are used in a calculation, SQL Server tries to convert it using implicit conversion behind our backs.
Did a conversion really happen? Besides, every column in the ExactNumerics1 table is a DECIMAL.
Let’s check the table structure of the ExactNumerics1 table in SQL Server Management Studio:
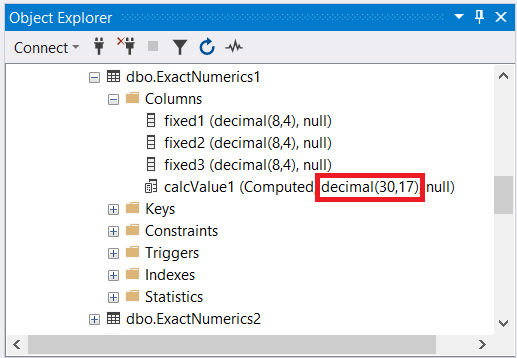
Notice the red boxed area in Figure 3. The computed column is a DECIMAL(30,17), not a DECIMAL(8,4). According to official documentation, 2 DECIMAL columns with different precision and scale are 2 different data types. See for yourself here. Because of the difference, a conversion is required. So, implicit conversion comes into play.
What if they are different and an implicit conversion had happened?
Again, based on the official documentation, a loss of precision or scale can happen during implicit conversion. Thus, an explicit CAST is required. Note the DECIMAL data type in the conversion table in that reference.
Some loss just happened here. If the calculated column is also DECIMAL(8,4), the implicit conversion does not occur.
To avoid the implicit conversion, follow the official documentation. The table structure should have been like this:
CREATE TABLE ExactNumerics2
(
fixed1 DECIMAL(8,4),
fixed2 DECIMAL(8,4),
fixed3 DECIMAL(8,4),
calcValue1 AS CAST(fixed3 / fixed1 * fixed2 AS DECIMAL(8,4)) -- the explicit CAST
)
The explicit CAST in the calculated column ensures that the data types are consistent. If we also follow this structure and insert the same data, the result will be correct. Check out the new output in Figure 6 below.
Eventually, exact numerics won’t be exact if an implicit conversion occurs between 2 or more DECIMAL values.
Why Knowing This is Important
It gives you an idea of what you need for your tables and variables. Moreover, implicit conversion can make even exact numerics go bonkers. So, explicitly define the precision and scale and be consistent with it in your calculations.
Should I Use SQL FLOAT for Financial Data?
When calculating percentages in every slice of a pie graph, the sum should be 100%. Totals in the summary and detailed reports should also be consistent. If the accuracy of results is crucial, an approximate data type like FLOAT won’t do the job. The logical choice for this is DECIMAL.
But a question remains.
When Should You Use FLOAT?
Use FLOAT for data that requires astronomical values like distances between galaxies. Meanwhile, the DECIMAL data type will suffer an arithmetic overflow with this type of data. Tiny values like the diameter of an atomic nucleus will also fit using FLOAT. Scientific data and other values that don’t require precision can also benefit from FLOAT.
Why Knowing This is Important
We don’t say that FLOAT is bad and DECIMAL is good or vice versa. Knowing the correct use cases for each will give you and your users the intended results. And then again, you want your users happy, right?
Conclusion
By the end of the day, we all want to do our jobs and be good at them. Math will always be part of our jobs. And knowing the correct numeric data types will also help us deal with it. It’s not hard if you know what you’re doing.
I hope this article has helped you avoid weird math in SQL Server.
Do you have anything else to add? Then, let us know in the Comments section. Share this also on your favorite social media platforms.
Tags: data types, sql errors Last modified: May 29, 2023









