Databases that serve business applications should often support temporal data. For example, suppose a contract with a supplier is valid for a limited time only. It can be valid from a specific point in time onward, or it can be valid for a specific time interval—from a starting time point to an ending time point. In addition, many times you need to audit all changes in one or more tables. You might also need to be able to show the state at a specific point in time or all changes made to a table in a specific period of time. From the data integrity perspective, you might need to implement many additional temporal specific constraints.
Introducing Temporal Data
In a table with temporal support, the header represents a predicate with an at least one-time parameter that represents the interval when the rest of the predicate is valid—the complete predicate is, therefore, a timestamped predicate. Rows represent timestamped propositions, and the row’s valid time period is typically expressed with two attributes: from and to, or begin and end.
Types of Temporal Tables
You might have noticed during the introduction part that there are two kinds of temporal issues. The first one is the validity time of the proposition – in which period the proposition that a timestamped row in a table represents was actually true. For example, a contract with a supplier was valid only from time point 1 to time point 2. This kind of validity time is meaningful to people, meaningful for the business. The validity time is also called application time or human time. We can have multiple valid periods for the same entity. For example, the aforementioned contract that was valid from time point 1 to time point 2 might also be valid from time point 7 to time point 9.
The second temporal issue is the transaction time. A row for the contract mentioned above was inserted at time point 1 and was the only version of the truth known to the database until somebody changed it, or even to the end of the time. When the row is updated at time point 2, the original row was known as being true to the database from time point 1 to time point 2. A new row for the same proposition is inserted with time valid for the database from time point 2 to the end of the time. The transaction time is also known as system time or database time.
Of course, you can also implement both application and system versioned tables. Such tables are called bitemporal tables.
In SQL Server 2016, you get support for the system time out of the box with system versioned temporal tables. If you need to implement application time, you need to develop a solution by yourself.
Allen’s Interval Operators
The theory for the temporal data in a relational model started to evolve more than thirty years ago. I will introduce quite a few useful Boolean operators and a couple of operators that work on intervals and return an interval. These operators are known as Allen’s operators, named after J. F. Allen, who defined a number of them in a 1983 research paper on temporal intervals. All of them are still accepted as valid and needed. A database management system could help you dealing with application times by implementing these operators out of the box.
Let me first introduce the notation I will use. I will work on two intervals, denoted i1 and i2. The beginning time point of the first interval is b1, and the end is e1; the beginning time point of the second interval is b2 and the end is e2. The Allen’s Boolean operators are defined in the following table.
[table id=2 /]
In addition to Boolean operators, there are Allen’s three operators that accept intervals as input parameters and return an interval. These operators constitute simple interval algebra. Note that those operators have the same name as relational operators you are probably already familiar with: Union, Intersect, and Minus. However, they don’t behave exactly like their relational counterparts. In general, using any of the three interval operators, if the operation would result in an empty set of time points or in a set that cannot be described by one interval, then the operator should return NULL. A union of two intervals makes sense only if the intervals meet or overlap. An intersection makes sense only if the intervals overlap. The Minus interval operator makes sense only in some cases. For example, (3:10) Minus (5:7) returns NULL because the result cannot be described by one interval. The following table summarizes the definition of the operators of interval algebra.
[table id=3 /]
Overlapping Queries Performance ProblemOne of the most complex operators to implement is the overlaps operator. Queries that need to find overlapping intervals are not simple to be optimized. However, such queries are quite frequent on temporal tables. In this and the next two articles, I will show you a couple of ways to optimize such queries. But before I introduce the solutions, let me introduce the problem.
In order to explain the problem, I need some data. The following code shows an example how to create a table with validity intervals expressed with the b and e columns, where the begin and the end of an interval are represented as integers. The table is populated with demo data from the WideWorldImporters.Sales.OrderLines table. Please note that there are multiple versions of the WideWorldImporters database, so you might get slightly different results. I used the WideWorldImporters-Standard.bak backup file from https://github.com/Microsoft/sql-server-samples/releases/tag/wide-world-importers-v1.0 to restore this demo database on my SQL Server instance.
Creating the Demo Data
I created a demo table dbo.Intervals in the tempd database with the following code.
USE tempdb; GO SELECT OrderLineID AS id, StockItemID * (OrderLineID % 5 + 1) AS b, LastEditedBy + StockItemID * (OrderLineID % 5 + 1) AS e INTO dbo.Intervals FROM WideWorldImporters.Sales.OrderLines; -- 231412 rows GO ALTER TABLE dbo.Intervals ADD CONSTRAINT PK_Intervals PRIMARY KEY(id); CREATE INDEX idx_b ON dbo.Intervals(b) INCLUDE(e); CREATE INDEX idx_e ON dbo.Intervals(e) INCLUDE(b); GO
Please note also the indexes created. The two indexes are optimal for searches on the beginning of an interval or on the end of an interval. You can check the minimal begin and maximal end of all intervals with the following code.
SELECT MIN(b), MAX(e) FROM dbo.Intervals;
You can see in the results that the minimal begin time point is 1 and maximal end time point is 1155.
Giving the Context to the Data
You might notice that I represent the beginning and ending time points as integers. Now I need to give the intervals some time context. In this case, a single time point represents a day. The following code creates a date lookup table and populates it. Note that the starting date is the 1st of July 2014.
CREATE TABLE dbo.DateNums (n INT NOT NULL PRIMARY KEY, d DATE NOT NULL); GO DECLARE @i AS INT = 1, @d AS DATE = '20140701'; WHILE @i <= 1200 BEGIN INSERT INTO dbo.DateNums (n, d) SELECT @i, @d; SET @i += 1; SET @d = DATEADD(day,1,@d); END; GO
Now, you can join the dbo.Intervals table to the dbo.DateNums table twice, to give the context to the integers that represent the beginning and the end of the intervals.
SELECT i.id, i.b, d1.d AS dateB, i.e, d2.d AS dateE FROM dbo.Intervals AS i INNER JOIN dbo.DateNums AS d1 ON i.b = d1.n INNER JOIN dbo.DateNums AS d2 ON i.e = d2.n ORDER BY i.id;
Introducing the Performance Problem
The problem with temporal queries is that when reading from a table, SQL Server can use only one index, and successfully eliminate rows that are not candidates for the result from one side only, and then scans the rest of the data. For example, you need to find all intervals in the table which overlap with a given interval. Remember, two intervals overlap when the beginning of the first one is lower or equal to the end of the second one and the beginning of the second one is lower or equal to the end of the first one, or mathematically when (b1 ≤ e2) AND (b2 ≤ e1).
The following query searched for all of the intervals that overlap with the interval (10, 30). Note that the second condition (b2 ≤ e1) is turned around to (e1 ≥ b2) for simpler reading (the beginning and the end of intervals from the table are always on the left side of the condition). The given, or the searched interval, is at the beginning of the timeline for all intervals in the table.
SET STATISTICS IO ON; DECLARE @b AS INT = 10, @e AS INT = 30; SELECT id, b, e FROM dbo.Intervals WHERE b <= @e AND e >= @b OPTION (RECOMPILE);
The query used 36 logical reads. If you check the execution plan, you can see that the query used the index seek in the idx_b index with the seek predicate [tempdb].[dbo].[Intervals].b <= Scalar Operator((30)) and then scan the rows and select the resulting rows using the residual predicate [tempdb].[dbo].[Intervals].[e]>=(10). Because the searched interval is at the beginning of the timeline, the seek predicate successfully eliminated the majority of the rows; only a few intervals in the table have the beginning point lower or equal to 30.
You would get similarly efficient query if the searched interval would be at the end of the timeline, just that SQL Server would use the idx_e index for seek. However, what happens if the searched interval is in the middle of the timeline, like the following query shows?
DECLARE @b AS INT = 570, @e AS INT = 590; SELECT id, b, e FROM dbo.Intervals WHERE b <= @e AND e >= @b OPTION (RECOMPILE);
This time, the query used 111 logical reads. With a bigger table, the difference with the first query would be even bigger. If you check the execution plan, you can find out that SQL Server used the idx_e index with the [tempdb].[dbo].[Intervals].e >= Scalar Operator((570)) seek predicate and [tempdb].[dbo].[Intervals].[b]<=(590) residual predicate. The seek predicate excludes approximately half of the rows from one side, while half of the rows from the other side is scanned and resulting rows extracted with the residual predicate.
Enhanced T-SQL Solution
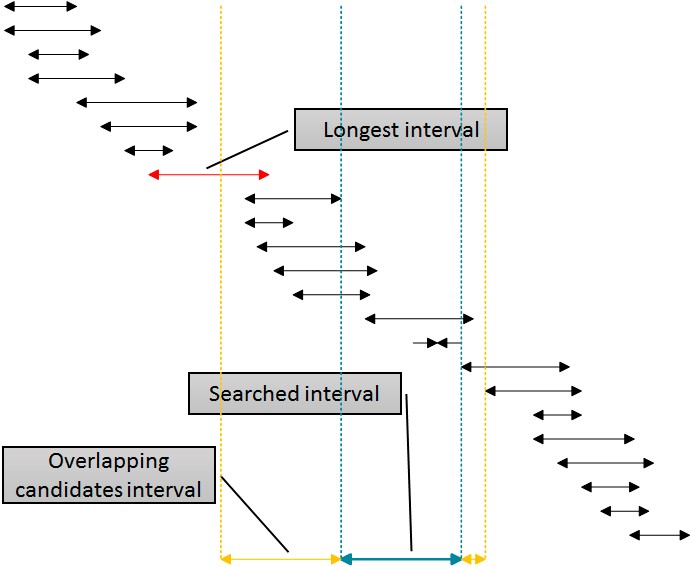
There is a solution which would use that index for the elimination of the rows from both sides of the searched interval by using a single index. The following figure shows this logic.
The intervals in the figure are sorted by the lower boundary, representing SQL Server’s usage of the idx_b index. Eliminating intervals from the right side of the given (searched) interval is simple: just eliminate all intervals where the beginning is at least one unit bigger (more to the right) of the end of the given interval. You can see this boundary in the figure denoted with the rightmost dotted line. However, eliminating from the left is more complex. In order to use the same index, the idx_b index for eliminating from the left, I need to use the beginning of the intervals in the table in the WHERE clause of the query. I have to go to the left side away from the beginning of the given (searched) interval at least for the length of the longest interval in the table, which is marked with a callout in the figure. The intervals that begin before the left yellow line cannot overlap with the given (blue) interval.
Since I already know that the length of the longest interval is 20, I can write an enhanced query in a quite simple way.
DECLARE @b AS INT = 570, @e AS INT = 590; DECLARE @max AS INT = 20; SELECT id, b, e FROM dbo.Intervals WHERE b <= @e AND b >= @b - @max AND e >= @b AND e <= @e + @max OPTION (RECOMPILE);
This query retrieves the same rows as the previous one with 20 logical reads only. If you check the execution plan, you can see that the idx_b was used, with the seek predicate Seek Keys[1]: Start: [tempdb].[dbo].[Intervals].b >= Scalar Operator((550)), End: [tempdb].[dbo].[Intervals].b <= Scalar Operator((590)), which successfully eliminated rows from both sides of the timeline, and then the residual predicate [tempdb].[dbo].[Intervals].[e]>=(570) AND [tempdb].[dbo].[Intervals].[e]<=(610) was used to select rows from a very limited partial scan.
Of course, the figure could be turned around to cover the cases when the idx_e index would be more useful. With this index, the elimination from the left is simple – eliminate all of the intervals which end at least one unit before the beginning of the given interval. This time, the elimination from the right is more complex – the end of the intervals in the table cannot be more to the right than the end of the given interval plus the maximal length of all intervals in the table.
Please note that this performance is the consequence of the specific data in the table. The maximal length of an interval is 20. This way, SQL Server can very efficiently eliminate intervals from both sides. However, if there would be only one long interval in the table, the code would become much less efficient, because SQL Server would not be able to eliminate a lot of rows from one side, either left or right, depending which index it would use. Anyway, in real life, interval length does not vary a lot many times, so this optimization technique might be very useful, especially because it is simple.
Conclusion
Please note that this is just one possible solution. You can find a solution that is more complex, yet it yields predictable performance no matter of the length of the longest interval in the Interval Queries in SQL Server article by Itzik Ben-Gan (http://sqlmag.com/t-sql/sql-server-interval-queries). However, I really like the enhanced T-SQL solution I presented in this article. The solution is very simple; all you need to do is to add two predicates to the WHERE clause of your overlapping queries. However, this is not the end of possibilities. Stay tuned, in the next two articles I will show you more solutions, so you will have a rich set of possibilities in your optimization toolbox.
Useful tool:
dbForge Query Builder for SQL Server – allows users to build quickly and easily complex SQL queries via an intuitive visual interface without manual code writing.