When developing an information system that also includes various processing of design and technological documentation, I faced the following problem.
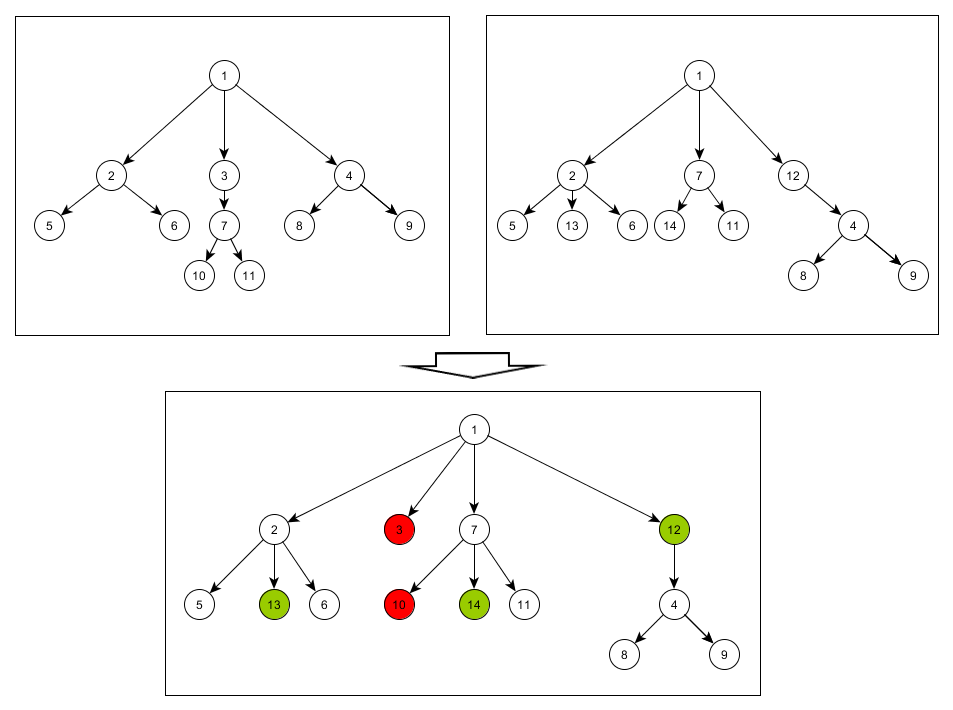
We have a certain product structure. During the day, different parts of this product are changed and by the evening, it is already unclear what has been changed. Sometimes, products can consist of more than 10 000 elements. The elements are not unique, and the reality is that the structure can be often modified, although the product is almost ready. The failure to understand the scope of changes complicates planning.
The product structure can be represented as a tree graph in PL/SQL. Since I could not find a suitable way to compare two graphs, I decided to create my own method.
Task
During the day, various changes are received by the accounting system from the design system. Production planning is based on the data from the accounting system. Conditions allow you to accept all the changes for the day and recalculate the product specification at night. However, as I wrote above, it is unclear how the yesterday state of the product differs from the today one.
I would like to see what was removed from the tree and what was added to it, as well as which part or assembly replaced another one. For example, if an intermediate node was added to the tree branch, it would be wrong to assume that all the downstream elements were removed from the old places and added to the new ones. They remained where they were, but the insert of the mediation node took place. In addition, the element can ‘travel’ up and down only within one branch of the tree due to the specifics of the manufacturing process.
Preparation
Product specification is recalculated by the PL/SQL-procedure within Oracle. That’s why I decided to create my own search of changes in PL/SQL.
The MR_ORDER_TREE table with the product tree looks in the following way:
[table id=21 /]
The item_ref, kts_item_id bindings are unique. In addition to the purchase, position, and quantity, there are other attributes of the particular element.
When recalculating the specification, data of the modified orders is completely deleted and recalculated. Therefore, it is necessary to keep the current tree state until the recalculation process starts. To do this, use the MR_ORDER_TREE_PREV table.
The comparison result will be stored in the MR_ORDER_TREE_COMP table, which will include two additional columns:
[table id=22 /]
Take the previous and current trees and add them to the MR_ORDER_TREE_COMP table. In addition, we will add a common root to the trees, increase item_id of the current tree by (a maximum value plus 1) item_id of the tree with the previous state. All the elements of the old tree will be considered as deleted, while the elements of the new tree – as inserted.
select nvl(max(item_id), 0) + 1
into v_id
from mr_order_tree_prev t
where t.order_id = p_order_id;
insert into MR_ORDER_TREE_COMP (ORDER_ID, ITEM_ID, KTS_ITEM_ID, ITEM_QTY,
IS_ITEM_BUY, IS_ADD_WORK, ITEM_POSITION, N_GROUP, T_LEVEL, STAT, COMM)
values (p_order_id, -1, null, 0, 0, 0, 0, 0, 0, -1, 'Additional data for calculation');
insert into MR_ORDER_TREE_COMP (ORDER_ID,
ITEM_ID,
ITEM_REF,
KTS_ITEM_ID,
KTS_ITEM_REF,
ITEM_QTY,
IS_ITEM_BUY,
IS_ADD_WORK,
ITEM_POSITION,
N_GROUP,
STAT,
COMM)
select p.order_id,
p.item_id,
nvl(p.item_ref, -1),
p.kts_item_id,
p.kts_item_ref,
p.item_qty,
p.is_item_buy,
p.is_add_work,
p.item_position,
p.n_group,
0,
'removal'
from mr_order_tree_prev p
where p.order_id = p_order_id;
insert into MR_ORDER_TREE_COMP (ORDER_ID,
ITEM_ID,
ITEM_REF,
KTS_ITEM_ID,
KTS_ITEM_REF,
ITEM_QTY,
IS_ITEM_BUY,
IS_ADD_WORK,
ITEM_POSITION,
N_GROUP,
STAT,
COMM)
select p.order_id,
p.item_id + v_id,
case
when p.item_ref is null
then -1
else p.item_ref + v_id
end,
p.kts_item_id,
p.kts_item_ref,
p.item_qty,
p.is_item_buy,
p.is_add_work,
p.item_position,
p.n_group,
1,
'insertion'
from mr_order_tree p
where p.order_id = p_order_id;
Specify the level of nesting for the elements of the summary tree so that you do not need to calculate it in the future.
for rec in (select item_id,
level lev
from (select *
from mr_order_tree_comp
where order_id = p_order_id)
connect by prior item_id = item_ref
start with item_id = -1)
loop
update mr_order_tree_comp c
set c.t_level = rec.lev
where c.order_id = p_order_id
and c.item_id = rec.item_id;
end loop;
Store the state of the mr_order_tree_comp table for the order to be recalculated. I used the collection, but I think it is possible to use a temporary table.
procedure save_tree_stat(p_order in number)
is
begin
select TREE_BC_STAT_ROW(c.order_id, c.item_id, c.item_ref, c.kts_item_id, c.kts_item_ref)
bulk collect into tree_before_calc
from mr_order_tree_comp c
where c.order_id = p_order;
end save_tree_stat;
“Addition” of trees
Now, we need to check the tree for changes by levels and nodes. First, determine the maximum level:
select max(t_level) into v_max_lvl from mr_order_tree_comp where order_id = p_order_id;
Now, we need to perform a cyclic check of the levels of this tree. At each level, we will select the child elements of each node, and look for an element with an “opposite sign”. In other words, we are going to look for kts_item_id with the same item_ref, but the state 1 is for 0 and 0 is for 1. After that, one of them is deleted, and the incoming elements are re-linked to the remaining node.
When the element is processed, insert it into a list of processed elements. To do this, I used the following procedure:
procedure add_to_rdy (p_item in number,
p_order in number)
is
begin
item_ready_list.extend;
item_ready_list(item_ready_list.last) := tree_rdy_list_row(p_order, p_item);
end add_to_rdy;
The following function processed the element:
function item_rdy(p_item in number, p_order in number) return number
The cycle looks like:
<<lvls>>
for i in 1..v_max_lvl
loop
<<heads>>
for rh in (select c.*
from mr_order_tree_comp c
where c.order_id = p_order_id
and c.t_level = i)
loop
<<leafs>>
for rl in (select c.*
from mr_order_tree_comp c
where c.order_id = p_order_id
and c.item_ref = rh.item_id
and c.stat in (0, 1)
order by c.stat)
loop
if (item_rdy(rl.item_id, rl.order_id) = 0) then
if (rl.stat = 0) then
select count(*)
into v_cnt
from mr_order_tree_comp c
where c.order_id = p_order_id
and c.item_ref = rh.item_id
and c.kts_item_id = rl.kts_item_id
and c.stat = 1;
case
when (v_cnt = 1) then
select c.item_id
into v_item
from mr_order_tree_comp c
where c.order_id = p_order_id
and c.item_ref = rh.item_id
and c.kts_item_id = rl.kts_item_id
and c.stat = 1;
update mr_order_tree_comp c
set c.item_ref = v_item
where c.item_ref = rl.item_id
and c.order_id = p_order_id;
update mr_order_tree_comp c
set c.stat = 4
where c.item_id = v_item
and c.order_id = p_order_id;
diff_items(p_order_id, rl.item_id, v_item);
delete mr_order_tree_comp c
where c.item_id = rl.item_id
and c.order_id = p_order_id;
add_to_rdy(rl.item_id, rl.order_id);
add_to_rdy(v_item, rl.order_id);
end case;
end if;
For (rl.stat = 1), the logic is the same.
When you find the same element, everything is simple – you just need to compare their properties. To do this, use the diff_items function. The situation, when more than one element is found, is an exception that indicates that something is wrong with the structure tree.
Search for identical elements
What to do when there was a change of one node to another, the node was inserted into the middle of the cycle or the node from the middle was removed?
To determine the described situations, I decided to compare the structures of two nodes in order to identify the ratio of the number of identical kts_item_id to the total number of elements. If the value of this ratio is greater than a certain value, the nodes are interchangeable. If the node has several replacement options at the current iteration of the cycle, the option with the highest “similarity index” is taken.
Let’s add a code to the main CASE.
when (v_cnt = 0) then
select count(*)
into v_cnt
from mr_order_tree_comp c
where c.order_id = p_order_id
and c.item_ref = rh.item_id
and c.stat = 1
and not exists (select 1
from table(item_ready_list) a
where a.order_id = c.order_id
and a.item_id = c.item_id);
I could find one element in this node.
if (v_cnt = 1) then
select c.item_id, c.kts_item_id
into v_item, v_kts
from mr_order_tree_comp c
where c.order_id = p_order_id
and c.item_ref = rh.item_id
and c.stat = 1
and not exists (select 1
from table(item_ready_list) a
where a.order_id = c.order_id
and a.item_id = c.item_id);
Without any hesitation, let’s link the contents of the current node to it provided that both elements are assemblies. The current element is not deleted. Why? If there are no identical elements in nodes at all, everything will be returned as unchanged.
if (is_item_comp(v_item, p_order_id) = is_item_comp(rl.item_id, p_order_id)) then
update mr_order_tree_comp c
set c.item_ref = v_item
where c.item_ref = rl.item_id
and c.order_id = p_order_id;
add_to_rdy(rl.item_id, rl.order_id);
add_to_rdy(v_item, rl.order_id);
end if;
end if;
If we could find several elements, we take the most suitable one. To define the similarity, use the like_degree procedure. The lperc variable contains the value of the index for comparison.
if (v_cnt > 1) then
begin
select item_id, kts_item_id, max_lperc
into v_item, v_kts, v_perc
from (select c.item_id,
c.kts_item_id,
max(like_degree(rl.item_id, c.item_id, c.order_id)) max_lperc
from mr_order_tree_comp c
where c.order_id = p_order_id
and c.item_ref = rh.item_id
and c.stat = 1
and not exists (select 1
from table(item_ready_list) a
where a.order_id = c.order_id
and a.item_id = c.item_id)
and is_item_comp(c.item_id, p_order_id) = (select is_item_comp(rl.item_id, p_order_id) from dual)
group by c.item_id, c.kts_item_id
order by max_lperc desc)
where rownum < 2;
if (v_perc >= lperc) then
update mr_order_tree_comp c
set c.item_ref = v_item
where c.item_ref = rl.item_id
and c.order_id = p_order_id;
update mr_order_tree_comp c
set c.comm = 'Removal. Replaced with ' || kts_pack.item_code(v_kts) || ' (' || to_char(v_perc) || '%)'
where c.item_id = rl.item_id
and c.order_id = p_order_id;
add_to_rdy(rl.item_id, rl.order_id);
add_to_rdy(v_item, rl.order_id);
end if;
end;
end if;
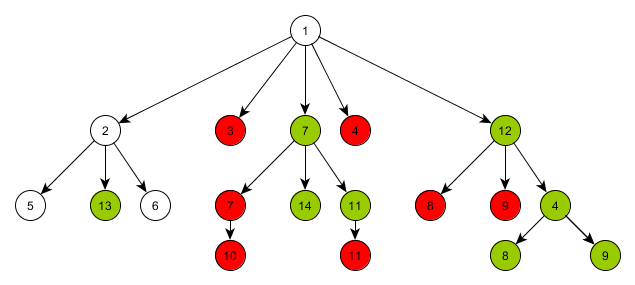
As a result, some elements will be relinked, and the tree will have the following structure:
If there is no need in using an additional root element that was added at the beginning, delete it.
You can take all the remaining elements with the status 0 and 1, and go up to the root. If you find the same element with the “opposite status”, then you need to compare them, remove the element with 0 from the tree, and change the status of the element with 1.
<<items>>
for rs in (select *
from mr_order_tree_comp c
where c.order_id = p_order_id
and c.stat in (0,1))
loop
<<branch>>
for rb in (select *
from (select *
from mr_order_tree_comp c
where c.order_id = p_order_id) t
connect by prior t.item_ref = t.item_id
start with t.item_id = rs.item_id)
loop
select count(*)
into v_cnt
from mr_order_tree_comp c
where c.item_ref = rb.item_id
and c.kts_item_id = rs.kts_item_id
and c.stat in (1,0)
and c.stat != rs.stat;
if (v_cnt = 1) then
select c.item_id
into v_item
from mr_order_tree_comp c
where c.item_ref = rb.item_id
and c.kts_item_id = rs.kts_item_id
and c.stat in (1,0)
and c.stat != rs.stat;
if (rs.stat = 0) then
update mr_order_tree_comp c
set c.stat = 4
where c.order_id = p_order_id
and c.item_id = v_item;
diff_items(p_order_id, rs.item_id, v_item);
update mr_order_tree_comp c
set c.item_ref = v_item
where c.order_id = p_order_id
and c.item_ref = rs.item_id;
delete mr_order_tree_comp
where order_id = p_order_id
and item_id = rs.item_id;
end if;
if (rs.stat = 1) then
update mr_order_tree_comp c
set c.stat = 4
where c.order_id = p_order_id
and c.item_id = rs.item_id;
diff_items(p_order_id, rs.item_id, v_item);
update mr_order_tree_comp c
set c.item_ref = rs.item_id
where c.order_id = p_order_id
and c.item_ref = v_item;
delete mr_order_tree_comp
where order_id = p_order_id
and item_id = v_item;
end if;
continue items;
end if;
end loop branch;
end loop items;
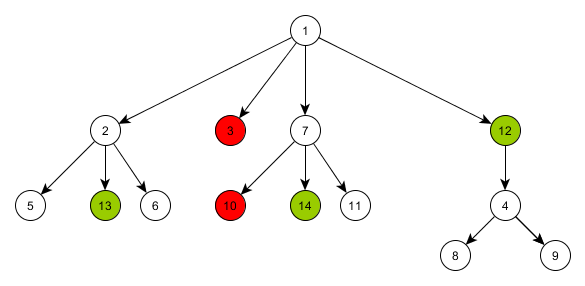
Now, go through the remaining elements with the status 0 and restore their previous item_ref. To do this, use the tree_before_calc collection, which stores the initial state of the mr_order_tree_comp tree.
The tree has the following structure:
I think there are more beautiful, fast and correct ways to compare trees. This is my method and hope it will be useful to someone.
Tags: oracle, sql Last modified: September 23, 2021