It is known, a computer can operate numbers with a limited number of bits. As a rule, we are accustomed to work with the 32-bit and 64-bit integers. On the .Net platform, the Int32 (int) and Int64 (long) types correspond to these integers.
But what to do if we need to represent, for instance, number 29! = 8841761993739701954543616000000? Such number won’t fit both 32-bit and 64-bit data types. Long arithmetic is designed specifically for working with such big numbers.
In computing technology, long arithmetic implies operations (addition, multiplication, subtraction, division, raising to a power etc.) with numbers, the bitness of which exceeds the length word of the given computer. These operations are implemented not by hardware but by software with the help of basic hardware for working with small-order numbers.
Long arithmetic can be also considered as one of the divisions of competitive programming since the bitness of standard types is quite often insufficient for representation of eventual result during problem solving. When choosing a programming language for the purposes of competitive programming, a set of tools (predefined libraries, implemented classed) built into the language, plays a pretty important role. Many languages (Java, Ruby, Python) have in-built support for long arithmetic that can drastically minimize time spent on writing a program.
Up to version 4.0, the .Net platform did not have the in-built support for working with long numbers. The .Net 4.0 platform supports both long and complex numbers. This functionality is available through the System.Numerics assembly and the BigInteger and Complex types defined in the namespace with the same name as the assembly.
The BigInteger structure was supposed to be included into .Net 3.5, but at that moment, it was not quite ready, and its implementation did not correspond to all the needs (performance problems were another factor). That’s why it was decided to postpone its release till .Net 4.0.
In this article, I would like to consider the details of the long arithmetic implementation from Microsoft.
General terms
The concept of the long numbers representation in computer memory is pretty straightforward. Let’s consider number 123456789 in decimal arithmetic. Obviously, it can be represented in the following way:
12345678910 = 1*108 + 2*107 + 3*106 + 4*105 + 5*104 + 6*103 + 7*102 + 8*101 + 9*100
Generally, any number can be represented as:
A = an-1βn-1 + an-2βn-2 +…+a1β + a0
where β – a numeric base, in which we represent the number, and the ai coefficients satisfy the two-sided inequality 0 ≤ ai < β.
The number representation resembles the polynomial representation, but instead of x raised to the corresponding power, we have the β base raised to the required power. As it is known, polynomial a0 + a1x + a2x2 + … + anxn can be conveniently represented as an array, elements of which represent coefficients ai and а, and index i defines the corresponding power of x. A long number is stored is the same way. The only thing left is to take a decision on the β base selection.
For instance, the same number 123456789 can be represented in decimal numeration (β = 104) system in the following way:
12345678910 = 1*(104)2 + 2345*(104)1 + 6789*(104)0
Representing number 123456789 in decimal numeration system gives us two benefits. First, we minimize the memory size consumed since instead of a 9-number array, it is enough to store a 3-number array (1, 2345 and 6789). Secondly, we considerably minimize the execution time for standard operations with long numbers, because 4-digit orders are processed simultaneously. In general, computer equally adds both one-figure numbers and 32-bit numbers, and therefore, it’s worth using it.
Usually, base β of a numeration system depends on a maximal size of base data type on a computer, and it is selected on the assumption of the following observations:
- Base must fit one of base data types;
- Base must be maximally large to decrease the size of a long number representation and increase the speed of operations with them, but at the same time small enough to ensure that all operations with coefficients use the base data type;
- For convenient output and debugging, β can be selected as a power of 10, β as a power of 2 allows performing low-level high-speed operations.
It is also worth mentioning that the number sign is covered by a separate variable, i.e. array contains the long number module, and the number is stored backward. It is made primarily for convenience: there is no need in processing null/last element of the array, in which the number sign could be stored, as well as all operations are executed in the ‘from junior to senior bits’ order.
BigInteger from Microsoft
If we take a look at the BigInteger structure through the Reflector or dotPeek decompiler, we will notice the following fields:
private static readonly BigInteger s_bnMinInt = new BigInteger(-1, new uint[1]{ (uint) int.MinValue });
private static readonly BigInteger s_bnOneInt = new BigInteger(1);
private static readonly BigInteger s_bnZeroInt = new BigInteger(0);
private static readonly BigInteger s_bnMinusOneInt = new BigInteger(-1);
internal int _sign;
internal uint[] _bits;
private const int knMaskHighBit = -2147483648;
private const uint kuMaskHighBit = 2147483648U;
private const int kcbitUint = 32;
private const int kcbitUlong = 64;
private const int DecimalScaleFactorMask = 16711680;
private const int DecimalSignMask = -2147483648;
The structure contains only two instance fields (_sign and _bits). The rest of fields are constants and static fields for reading that provide structure values for numbers -1, 0 and 1.
We can assume that the _sign variable stores number sign, and the _bits array contains the ai coefficients. Taking into account that the _bits array is of the uint[] type, we can suggest that the power of two 232 is taken as a β base (since uint is a 32-bit unsigned number).
So, let’s try to prove or disprove our suggestions.
A constructor taking int as an argument looks in the following way:
public BigInteger(int value)
{
if (value == int.MinValue)
{
this = BigInteger.s_bnMinInt;
}
else
{
this._sign = value;
this._bits = (uint[]) null;
}
}
Its implementation can tell a bit more about the role of the _sign variable. As we can see, if a long number fits the int range (from -231 to 231-1), it is stored in the _sign variable. And the _bits array is not used at all and is equal to null. This optimization should speed up the work of the BigInteger type as well as decrease the size of consumed memory when the number, in fact, is not large.
A constructor taking unit as an argument looks in the following way:
public BigInteger(uint value)
{
if (value <= (uint) int.MaxValue)
{
this._sign = (int) value;
this._bits = (uint[]) null;
}
else
{
this._sign = 1;
this._bits = new uint[1];
this._bits[0] = value;
}
}
Depending on whether the number fits the range or it does not, it is written into either the _sign variable, or into the _bits array.
The next constructor taking the 64-bit number with a sign (long) helps to answer the question on the choice of numeric base:
public BigInteger(long value)
{
if ((long) int.MinValue <= value && value <= (long) int.MaxValue)
{
if (value == (long) int.MinValue)
{
this = BigInteger.s_bnMinInt;
}
else
{
this._sign = (int) value;
this._bits = (uint[]) null;
}
}
else
{
ulong num;
if (value < 0L) { num = (ulong) -value; this._sign = -1; } else { num = (ulong) value; this._sign = 1; } this._bits = new uint[2]; this._bits[0] = (uint) num; this._bits[1] = (uint) (num >> 32);
}
}
If a number does not fit the int range, the _sign variable, as we see, contains the number sign (-1 – for negative, and 1 – for positive), and the _bits array contains the same ai coefficients and is filled in the following way:
this._bits = new uint[2]; this._bits[0] = (uint) num; this._bits[1] = (uint) (num >> 32);
In this case, the 64-bit num number is divided into two 32-bit numbers (uint)num и (uint)(num >> 32). The first number is the last 32 bits of the num number, whereas the second number represents the first 32 bits (right shift at n bits matches the integer division by 2n).
Let’s define how the long.MaxValue = 263-1 = 9223372036854775807 number will be stored in the BigInteger structure. For this, let’s divide it by 232:
In fact, (uint)long.MaxValue = 4294967295, (uint)(long.MaxValue >> 32) = 2147483647.
Therefore, 9223372036854775807 = 2147483647*(232)1 + 4294967295*(232)0, and BigInteger will be represented by a pair:
_sign = 1
_bits = {4294967295, 2147483647} // keep in mind that the number is stored backwards
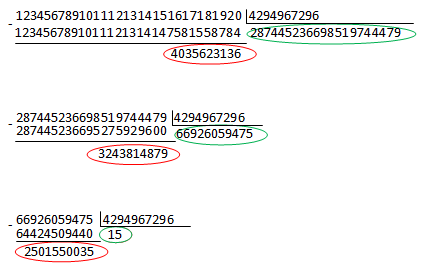
For the long number -1234567891011121314151617181920, we have:
That is, the number is expanded in powers of 232 in the following way:
1234567891011121314151617181920 = 15*(232)3 + 2501550035*(232)2 + 3243814879*(232)1 + 4035623136*(232)0
Therefore, BigInteger will be represented by a pair:
_sign = -1 // number sign
_bits = {4035623136, 3243814879, 2501550035, 15}
The number that fits the int range, let’s say 17, will be stored in the following way:
_sign = 17
_bits = null
Having studied the BigInteger constructors and structures, we can conclude the following:
- If a number fits the int range, it is stored in the _sign variable;
- If a number does not fit the int range, its sign is stored in the _sign variable (-1 for a negative number, and 1 for a positive number), and the _bits array stores the ai coefficients of the long number expansion with base 232.
The β = 232 base is a good choice since it is easier to work with the power of two on the low level (multiplication and division by the power of two correspond to the bit left and right shifts), as well as allows to quickly perform operations with them.
In general, the BigInteger structure is a full-featured implementation of the long arithmetic on the .Net platform. In addition, Microsoft tried to bring it maximally closer to primitive numeric types: a BigInteger instance can be used in the same way as any other integer type. BigInteger reloads standard numeric operations for execution of basic mathematical operations, such as addition, subtraction, division, multiplication, subtractions, negation, and unary negation. We can also use standard numeric operators for comparing two BigInteger values with each other. Similarly to other integer types, BigInteger supports bit operators: And, Or, XOR, left shift, right shift.
For languages that do not support the user-defined operators, the BigInteger structure also provides equivalent methods for execution of mathematical operations. It refers to methods dd, Divide, Multiply, Negate, Subtract, and some other methods. Microsoft treated the implementation of the Decimal structure in the same way.
Many members of the BigInteger structure directly correspond to members of other integer types. Besides, BigInteger adds such elements as:
- IsEven – defines whether a number is even;
- IsPowerOfTwo — defines whether a number is a power of two;
- Sign — returns a value that specifies the BigInteger sign number;
- Abs — returns the absolute value of the BigIneger number;
- DivRem — returns quotient and remainder after division operation;
- GreatestCommonDivisor — returns the largest common divisor for two numbers;
- Log — returns logarithm of the specified number in a numeration system with specified base;
- Max/Min — returns the largest/smallest of two numbers;
- ModPow — executes modular division of a number that is raised to power of another number;
- Pow — raises the BigInteger value to the specified power.
Few words on BigInteger in Mono and Java
It is notable that Mono also supports long arithmetic. Implementation of the BigInteger structure in Mono is practically the same as in Microsoft, except for the absence of optimization of numbers represented by the int type.
That is, number 17 in Mono will by represented by the following pair:
_sign = 1 // number sign
_bits = {17}
BigInteger is implemented in Java in the similar way:
public class BigInteger extends Number implements Comparable
{
int signum;
int[] mag;
private int bitCount = -1;
private int bitLength = -1;
private int lowestSetBit = -2;
private int firstNonzeroByteNum = -2;
private int firstNonzeroIntNum = -2;
private final static long LONG_MASK = 0xffffffffL;
}
Since there are no unsigned types in Java, the mag array is of the int[] type. Therefore, representation of a long number in Java and .Net differ. In .Net, the representation will be more effective, since the unit type covers bigger range:
private BigInteger(long val)
{
if (val < 0) { signum = -1; val = -val; } else { signum = 1; } int highWord = (int)(val >>> 32);
if (highWord == 0) {
mag = new int[1];
mag[0] = (int)val;
}
else {
mag = new int[2];
mag[0] = highWord;
mag[1] = (int)val;
}
}
Java as well as Mono does not have optimization for numbers represented by the int type.
BigInteger Productivity
When you work with the BigInteger long numbers, you should bear in mind possible productivity-related problems. For example, a seemingly harmless ++ operator may considerably affect productivity:
int length = 1000000;
BigInteger num = BigInteger.Parse("12345678910111213141516171819");
for (int i = 2; i < length; i++)
{
if (IsPrime(i))
num++;
}
Console.WriteLine(num);
Though it seems that the value change takes place in the given example, it is not the case. The BigInteger objects are immutable, i.e. in fact, common language runtime internally creates a new BigInteger object and assigns a value to it that is a unit bigger than the previous one.
In the given example, we can proceed in the following way: execute intermediate operations with the normal number types, and then use BigInteger:
int length = 1000000;
BigInteger num = BigInteger.Parse("12345678910111213141516171819");
int temp = 0;
for (int i = 2; i < length; i++)
{
if (IsPrime(i))
temp++;
}
num += temp;
Console.WriteLine(num);
Other .NET Framework number types are immutable as well. However, since the BigInteger types do not have upper or lower bounds, its values may increase to very large values and have a measurable impact on productivity.
Instead of conclusion
As from version 4, .Net includes the full-featured implementation of integer-valued long arithmetic. The only thing it lacks is, probably, implementation of the BigRational structure that has been present in .Net BCL in beta state for a long time.
The description of the BigRational structure: the BigRational structure is based on the BigInteger that was introduced in .Net Framework 4 and allows creating arbitrary-precision rational numbers. A rational number is a ratio between two integers, and in this implementation of the BigRational structure, the BigInteger is used as the numerator and denominator.
Tags: .net, .net framework, c# Last modified: September 23, 2021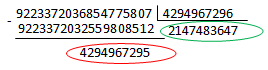






You should try dnSpy for decompiling, it will blow your mind.