Sorting is a typical task each programmer should be aware of. That’s why this article is dedicated to the implementation of sorting in .NET. I will describe how array sorting works in .NET, its aspects, and make a small comparison with sorting in Java.
Let’s begin with the fact that the first versions of .NET use the quicksort algorithm by default. So, let’s consider pros and cons of the quicksort.
Pros
- One of the most high-performance algorithms(on a practical level) of general-purpose internal sorting.
- Easy implementation.
- Requires just O(logn) of additional memory for its operation.
- Can be easily combined with caching and internal memory mechanisms.
Cons
- Heavily decreases in speed down to O(n2) in the case of unsuccessful pivot selections. This may happen in the case of unsuccessful input data. To prevent such situations, we need to select a pivot accidentally, not in a fixed way.
- Lame implementation of the algorithm may result in stack overflow error, since it may require O(n) embedded recursive calls. In improved implementations, where recursive call takes place only for sorting of the smaller part of an array, the recursion depth does not exceed O(logn).
- It is unstable. If stability is required, a key must be expanded.
The lame implementation may look in the following way:
public void QuickSort(int left, int right)
{
int l = left;
int r = right;
int avg = array[(l + r) / 2)];
do
{
while (array[l] < avg) ++l; while (array[r] > avg)
--r;
if (l <= r)
{
if (l < r)
{
int temp = array[l];
array[l] = array[r];
array[r] = temp;
}
++l;
--r;
}
}
while (l <= r);
if (left < r)
QuickSort(left, r);
if (l < right)
QuickSort(l, right);
}
The above algorithm has the following cons:
- Since pivot is selected as the middle of an array, it may be the case that it always will be the maximum. As a result, an array will be divided into two parts of n — 1 and 1 in length, and the algorithm speed will decrease to O(n2).
- Under the specified conditions, the recursion depth reaches O(n). As a result, software stack overflow may take place if n values are large.
- The algorithm is unstable. That is, it modifies elements with similar values. If we sort numbers, it does not have any effect. But if we sort an array of objects by some property, it has vital importance, as several calls of the Sort method may result in an array with elements of different order.
Sorting Implementation in .NET
.NET 1.0
Let’s see what happens in .NET 1.0. Leaping ahead, I can say that we won’t see anything positive here, especially for user-defined value types (in particular, because of the lack of generalizations).
public static void Sort(Array array)
{
Array.Sort(array, (Array) null, array.GetLowerBound(0), array.Length, (IComparer) null);
}
public static void Sort(Array keys, Array items, int index, int length, IComparer comparer)
{
if (length > 1) {
if (comparer == Comparer.Default || comparer == null) {
if(TrySZSort(array, null, index, index + length - 1)) {
return;
}
}
object[] keys1 = keys as object[];
object[] items1 = (object[]) null;
if (keys1 != null)
items1 = items as object[];
if (keys1 != null && (items == null || items1 != null))
new Array.SorterObjectArray(keys1, items1, comparer).QuickSort(index, index + length - 1);
else
new Array.SorterGenericArray(keys, items, comparer).QuickSort(index, index + length - 1);
}
Now, let’s take a look at the SorterObjectArray and SorterGenericArray classes:
SorterObjectArray
private class SorterObjectArray
{
private object[] keys;
private object[] items;
private IComparer comparer;
public SorterObjectArray(object[] keys, object[] items, IComparer comparer)
{
if (comparer == null)
comparer = (IComparer)Comparer.Default;
this.keys = keys;
this.items = items;
this.comparer = comparer;
}
public virtual void QuickSort(int left, int right)
{
do
{
int left1 = left;
int right1 = right;
object obj1 = this.keys[left1 + right1 >> 1];
do
{
while (this.comparer.Compare(this.keys[left1], obj1) < 0)
++left1;
while (this.comparer.Compare(obj1, this.keys[right1]) < 0)
--right1;
if (left1 <= right1)
{
if (left1 < right1)
{
object obj2 = this.keys[left1];
this.keys[left1] = this.keys[right1];
this.keys[right1] = obj2;
if (this.items != null)
{
object obj3 = this.items[left1];
this.items[left1] = this.items[right1];
this.items[right1] = obj3;
}
}
++left1;
--right1;
}
else
break;
}
while (left1 <= right1);
if (right1 - left <= right - left1)
{
if (left < right1)
this.QuickSort(left, right1);
left = left1;
}
else
{
if (left1 < right)
this.QuickSort(left1, right);
right = right1;
}
}
while (left < right);
}
}
SorterGenericArray
private class SorterGenericArray
{
private Array keys;
private Array items;
private IComparer comparer;
public SorterGenericArray(Array keys, Array items, IComparer comparer)
{
if (comparer == null)
comparer = (IComparer)Comparer.Default;
this.keys = keys;
this.items = items;
this.comparer = comparer;
}
public virtual void QuickSort(int left, int right)
{
do
{
int num1 = left;
int num2 = right;
object obj1 = this.keys.GetValue(num1 + num2 >> 1);
do
{
while (this.comparer.Compare(this.keys.GetValue(num1), obj1) < 0)
++num1;
while (this.comparer.Compare(obj1, this.keys.GetValue(num2)) < 0)
--num2;
if (num1 <= num2)
{
if (num1 < num2)
{
object obj2 = this.keys.GetValue(num1);
this.keys.SetValue(this.keys.GetValue(num2), num1);
this.keys.SetValue(obj2, num2);
if (this.items != null)
{
object obj3 = this.items.GetValue(num1);
this.items.SetValue(this.items.GetValue(num2), num1);
this.items.SetValue(obj3, num2);
}
}
++num1;
--num2;
}
else
break;
}
while (num1 <= num2);
if (num2 - left <= right - num1)
{
if (left < num2)
this.QuickSort(left, num2);
left = num1;
}
else
{
if (num1 < right)
this.QuickSort(num1, right);
right = num2;
}
}
while (left < right);
}
}
So, what does actually happen here? The following code:
object[] keys1 = keys as object[]; object[] items1 = (object[]) null; if (keys1 != null) items1 = items as object[];
is nothing else but an attempt to use array covariance that works only for referenced types. So, the SorterObjectArray class is used for referenced types, while the SorterGenericArray class is used for value types. But what is the difference between the classes? The only difference is the method of accessing array elements. The slow GetValue and SetValue methods are used for value types. So, will an array of integers be sorted very long (since integer is a value type)? No! It is sorted very fast because of the following code:
if (length > 1) {
if (comparer == Comparer.Default || comparer == null) {
if(TrySZSort(array, null, index, index + length - 1))
return;
} }
The Array.TrySZSort method is interesting, in particular. This method calls the native sorting implemented on С++ in CLR itself. It works for primitive types when we use the standard logic of element comparison. That is, when comparer == Comparer.Default || comparer == null.
The native implementation looks in the following way:
Native TrySZSort
FCIMPL4(INT32, ArrayHelper::TrySZSort, ArrayBase * keys, ArrayBase * items, UINT32 left, UINT32 right)
//in an array is not single-dimensional with initial index, null is not sorted
if (keys->GetRank() != 1 || keys->GetLowerBoundsPtr()[0] != 0)
return FALSE;
// Getting array element type
TypeHandle keysTH = keys->GetElementTypeHandle();
// If it is not an in-built primitive type
const CorElementType keysElType = keysTH.GetSigCorElementType();
if (!CorTypeInfo::IsPrimitiveType(keysElType))
return FALSE;
if (items != NULL) {
TypeHandle itemsTH = items->GetElementTypeHandle();
if (keysTH != itemsTH)
return FALSE; // Can't currently handle sorting different types of arrays.
}
// Optimization for the array from one element
if (left == right || right == 0xffffffff)
return TRUE;
//Then the special version of sorting is called that is written on the basis of the C++ templates.
switch(keysElType) {
case ELEMENT_TYPE_I1: // 1-byte signed integer(sbyte)
ArrayHelpers::QuickSort((I1*) keys->GetDataPtr(), (I1*) (items == NULL ? NULL : items->GetDataPtr()), left, right);
break;
case ELEMENT_TYPE_U1: // 1-byte unsigned integer(byte)
case ELEMENT_TYPE_BOOLEAN: // Логический тип (bool)
ArrayHelpers::QuickSort((U1*) keys->GetDataPtr(), (U1*) (items == NULL ? NULL : items->GetDataPtr()), left, right);
break;
case ELEMENT_TYPE_I2: // 2-byte signed integer (short)
ArrayHelpers::QuickSort((I2*) keys->GetDataPtr(), (I2*) (items == NULL ? NULL : items->GetDataPtr()), left, right);
break;
case ELEMENT_TYPE_U2: // 2-byte unsigned integer (ushort)
case ELEMENT_TYPE_CHAR: // Character type (char)
ArrayHelpers::QuickSort((U2*) keys->GetDataPtr(), (U2*) (items == NULL ? NULL : items->GetDataPtr()), left, right);
break;
case ELEMENT_TYPE_I4: // 4-byte signed integer (int)
ArrayHelpers::QuickSort((I4*) keys->GetDataPtr(), (I4*) (items == NULL ? NULL : items->GetDataPtr()), left, right);
break;
case ELEMENT_TYPE_U4: // 4-byte unsigned integer (uint)
ArrayHelpers::QuickSort((U4*) keys->GetDataPtr(), (U4*) (items == NULL ? NULL : items->GetDataPtr()), left, right);
break;
case ELEMENT_TYPE_R4: // 4-byte floating point number (float)
ArrayHelpers::QuickSort((R4*) keys->GetDataPtr(), (R4*) (items == NULL ? NULL : items->GetDataPtr()), left, right);
break;
case ELEMENT_TYPE_I8: // 8-byte signed integer (long)
ArrayHelpers::QuickSort((I8*) keys->GetDataPtr(), (I8*) (items == NULL ? NULL : items->GetDataPtr()), left, right);
break;
case ELEMENT_TYPE_U8: // 8-byte unsigned integer(ulong)
ArrayHelpers::QuickSort((U8*) keys->GetDataPtr(), (U8*) (items == NULL ? NULL : items->GetDataPtr()), left, right);
break;
case ELEMENT_TYPE_R8: // 8-byte floating point number (double)
ArrayHelpers::QuickSort((R8*) keys->GetDataPtr(), (R8*) (items == NULL ? NULL : items->GetDataPtr()), left, right);
break;
case ELEMENT_TYPE_I: // Dimension of integer in machine code (IntPtr)
case ELEMENT_TYPE_U: // Dimension of unsigned integer in machine code (UIntPtr)
// In V1.0, IntPtr & UIntPtr are not fully supported types. They do
// not implement IComparable, so searching & sorting for them should
// fail. In V1.1 or V2.0, this should change.
return FALSE;
default:
return FALSE;
}
return TRUE;
}
Native QuickSort
/ Template class designed for sorting
template
class ArrayHelpers
{
static void QuickSort(KIND keys[], KIND items[], int left, int right) {
do {
int i = left;
int j = right;
KIND x = keys[(i + j) >> 1];
do {
while (Compare(keys[i], x) < 0) i++;
while (Compare(x, keys[j]) < 0) j--; if (i > j) break;
if (i < j) {
KIND key = keys[i];
keys[i] = keys[j];
keys[j] = key;
if (items != NULL) {
KIND item = items[i];
items[i] = items[j];
items[j] = item;
}
}
i++;
j--;
}
while (i <= j);
if (j - left <= right - i)
{
if (left < j) QuickSort(keys, items, left, j);
left = i;
}
else
{
if (i < right) QuickSort(keys, items, i, right);
right = j;
}
}
while (left < right);
}
};
As you see, the native sorting works only for primitive types, including all numeric types+logical type+character type. As for the user-defined types, everything will work extremely slow.
Let’s consider the implementation of the sorting algorithm as such. We will consider its implementation in the SorterObjectArray class since the native implementation and the implementation for value types are similar.
1. An array middle is always taken as a pivot:
object obj1 = this.keys[left1 + right1 >> 1];
When input data is bad, the algorithm execution time may become quadratic. Besides, the middle is taken on the basis of the formula num1 + num2 >> 1 that may result in the int type overflow. The same error has been made in binary search and sorting algorithm in Java (link to the bug).
This problem has not been fixed in the next versions of Java.
2. To avoid stack overflow, this implementation has an optimization that eliminates one recursion branch. Instead of calling recursive division procedure for both found subarrays after array division, the recursive call is made only for smaller subarray, while the bigger one is processed in a loop within the same procedure call. In terms of efficiency, there is no difference in the average case: the overhead cost of additional recursive call and length comparison of subarrays and the loop are approximately the same. Meanwhile, the recursion depth never exceeds log2n, and in the worst case of confluent division, it will be no more than 2 – the whole processing will be held within the loop of the first level of recursion.
.NET 2.0
The new implementation features slight changes. Since generalizations have been introduced in .NET 2.0, I will use the generalized version of sorting.
public static void Sort(T[] array, int index, int length, IComparer comparer)
{
// TrySZSort is still faster than generalized implementation.
// The reason is that a call of the Int32.CompareTo method is executed slower than "<" or ">".
if (length <= 1 || (comparer == null || comparer == Comparer.Default) &&
Array.TrySZSort((Array) array, (Array) null, index, index + length - 1))
return;
ArraySortHelper.Default.Sort(array, index, length, comparer);
}
The sorting method itself looks in the following way:
private static void SwapIfGreaterWithItems(T[] keys, IComparer comparer, int a, int b)
{
if (a == b || comparer.Compare(keys[a], keys[b]) <= 0)
return;
T obj = keys[a];
keys[a] = keys[b];
keys[b] = obj;
}
internal static void QuickSort(T[] keys, int left, int right, IComparer comparer)
{
do
{
int index1 = left;
int index2 = right;
int index3 = index1 + (index2 - index1 >> 1);
ArraySortHelper.SwapIfGreaterWithItems(keys, comparer, index1, index3);
ArraySortHelper.SwapIfGreaterWithItems(keys, comparer, index1, index2);
ArraySortHelper.SwapIfGreaterWithItems(keys, comparer, index3, index2);
T obj1 = keys[index3];
do
{
while (comparer.Compare(keys[index1], obj1) < 0)
++index1;
while (comparer.Compare(obj1, keys[index2]) < 0)
--index2;
if (index1 <= index2)
{
if (index1 < index2)
{
T obj2 = keys[index1];
keys[index1] = keys[index2];
keys[index2] = obj2;
}
++index1;
--index2;
}
else
break;
}
while (index1 <= index2);
if (index2 - left <= right - index1)
{
if (left < index2)
ArraySortHelper.QuickSort(keys, left, index2, comparer);
left = index1;
}
else
{
if (index1 < right)
ArraySortHelper.QuickSort(keys, index1, right, comparer);
right = index2;
}
}
while (left < right);
}
Optimization for in-built primitive types still exists despite the availability of generalizations. Thus, primitive types still use native sorting.
Now, the median of the first, middle and last elements of an array is taken as a pivot instead of the array middle.
int index3 = index1 + (index2 - index1 >> 1); //the middle ArraySortHelper.SwapIfGreaterWithItems(keys, comparer, index1, index3); ArraySortHelper.SwapIfGreaterWithItems(keys, comparer, index1, index2); ArraySortHelper.SwapIfGreaterWithItems(keys, comparer, index3, index2); T obj1 = keys[index3];
Besides, now the middle is calculated according to the formula index1 + (index2 — index1 >> 1) that eliminates overflow errors.
The rest has been left intact.
Now, let’s suppose we need to sort an array of integers in descending order. How will you do it?
On my computer, the following code:
Array.Sort(a); Array.Reverse(a);
works approximately 3 times faster than
Array.Sort(a, (x, y) => -x.CompareTo(y))
You may be confused with the fact that the Array.Reverse method is not generalized, which means that it will work slowly with the value types (packaging and the GetValue, SetValue methods). But if we look at its implementation, we will see optimization for built-in value types. In particular, it will call the Array.TrySZReverse native method that looks in the following way:
template
static void Reverse(KIND array[], UINT32 index, UINT32 count) {
if (count == 0) {
return;
}
UINT32 i = index;
UINT32 j = index + count - 1;
while(i < j) {
KIND temp = array[i];
array[i] = array[j];
array[j] = temp;
i++;
j--;
}
}
};
In general, we can find generalizations everywhere in the standard library. And it’s strange that there is no a generic version of this method. There is the Reverse method as an extension method of Enumerable, but its disadvantage is that it makes this not on site. So, the call of Array.Reverse on an array of user-defined value types always results in autoboxing.
.NET 3.0 — .NET 4.0
The algorithm has not been changed.
.NET 4.5
Before we start considering the algorithm, I’d like to say a few words about the deployment of .NET 4.5. I highly recommend you to have a look at this article in this regard. When installing VS 2012, i.e. when installing NET 4.5, it replaces assemblies of the 4th framework. In fact, it means that even if you are coding on .NET 4, you are using the .NET 4.5 assemblies. So, before the installation of 4.5, you use one sorting algorithm, and after installation, you use the other algorithm, and it happens without your knowing.
To find out what is happening, let’s have a look at the following code from .NET 4.5:
public void Sort(T[] keys, int index, int length, IComparer comparer)
{
if (BinaryCompatibility.TargetsAtLeast_Desktop_V4_5)
ArraySortHelper.IntrospectiveSort(keys, index, length, comparer);
else
ArraySortHelper.DepthLimitedQuickSort(keys, index, length + index - 1, comparer, 32);
}
As you see, the method includes checking the .NET version: if it is 4.5, we use IntrospectiveSort, if it is 4.0, we use DepthLimitedQuickSort.
Let’s find out how DepthLimitedQuickSort differs from the sorting used in .NET 4.0 before the VS 2012 installation. Let’s take a look at the code of the method:
internal static void DepthLimitedQuickSort(T[] keys, int left, int right, IComparer comparer, int depthLimit)
{
while (depthLimit != 0)
{
int index1 = left;
int index2 = right;
int index3 = index1 + (index2 - index1 >> 1);
ArraySortHelper.SwapIfGreater(keys, comparer, index1, index3);
ArraySortHelper.SwapIfGreater(keys, comparer, index1, index2);
ArraySortHelper.SwapIfGreater(keys, comparer, index3, index2);
T obj1 = keys[index3];
do
{
while (comparer.Compare(keys[index1], obj1) < 0)
++index1;
while (comparer.Compare(obj1, keys[index2]) < 0)
--index2;
if (index1 <= index2)
{
if (index1 < index2)
{
T obj2 = keys[index1];
keys[index1] = keys[index2];
keys[index2] = obj2;
}
++index1;
--index2;
}
else
break;
}
while (index1 <= index2);
--depthLimit;
if (index2 - left <= right - index1)
{
if (left < index2)
ArraySortHelper.DepthLimitedQuickSort(keys, left, index2, comparer, depthLimit);
left = index1;
}
else
{
if (index1 < right)
ArraySortHelper.DepthLimitedQuickSort(keys, index1, right, comparer, depthLimit);
right = index2;
}
if (left >= right)
return;
}
ArraySortHelper.Heapsort(keys, left, right, comparer);
}
As you can see, it is the same quicksort except for one thing: the algorithm switches to the heapsort if we exhaust recursion depth that equals 22 by default.
The heapsort looks in the following way:
private static void Heapsort(T[] keys, int lo, int hi, IComparer comparer)
{
int n = hi - lo + 1;
for (int i = n / 2; i >= 1; --i)
ArraySortHelper.DownHeap(keys, i, n, lo, comparer);
for (int index = n; index > 1; --index)
{
ArraySortHelper.Swap(keys, lo, lo + index - 1);
ArraySortHelper.DownHeap(keys, 1, index - 1, lo, comparer);
}
}
private static void DownHeap(T[] keys, int i, int n, int lo, IComparer comparer)
{
T x = keys[lo + i - 1];
for (; i <= n / 2; { int num; i = num;})
{
num = 2 * i;
if (num < n && comparer.Compare(keys[lo + num - 1], keys[lo + num]) < 0)
++num;
if (comparer.Compare(x, keys[lo + num - 1]) < 0)
keys[lo + i - 1] = keys[lo + num - 1];
else
break;
}
keys[lo + i - 1] = x;
}
The DepthLimitedQuickSort algorithm is nothing but IntroSort.
Introsort or introspective sort is a hybrid sorting algorithm that provides both fast average performance and (asymptotically) optimal worst-case performance. It begins with quicksort and switches to heapsort when the recursion depth exceeds a level based on (the logarithm of) the number of elements being sorted. This combines the good parts of both algorithms, with practical performance comparable to quicksort on typical data sets and worst-case O(n log n) runtime due to the heap sort. Since both algorithms it uses are comparison sorts, it too is a comparison sort.
Now, let’s look at IntrospectiveSort. In fact, this is the same introspective sorting, but more optimized. By the way, MSDN still states it uses quicksort.
IntroSort
private static void IntroSort(T[] keys, int lo, int hi, int depthLimit, IComparer comparer)
{
for (; hi > lo; {int num; hi = num - 1;})
{
int num = hi - lo + 1;
if (num <= 16) //if there are less that 16 elements, use insertion sorting
{
if (num == 1) //if there is one element
break;
if (num == 2) //if there are two elements
{
ArraySortHelper.SwapIfGreater(keys, comparer, lo, hi);
break;
}
else if (num == 3) //if there are three elements
{
ArraySortHelper.SwapIfGreater(keys, comparer, lo, hi - 1);
ArraySortHelper.SwapIfGreater(keys, comparer, lo, hi);
ArraySortHelper.SwapIfGreater(keys, comparer, hi - 1, hi);
break;
}
else
{
ArraySortHelper.InsertionSort(keys, lo, hi, comparer); //insertion sort
break;
}
}
else if (depthLimit == 0) //if recursion depth has been exhausted
{
ArraySortHelper.Heapsort(keys, lo, hi, comparer); //using heap sorting
break;
}
else // otherwise, we use partitioning of quick sort
{
--depthLimit;
num = ArraySortHelper.PickPivotAndPartition(keys, lo, hi, comparer);
ArraySortHelper.IntroSort(keys, num + 1, hi, depthLimit, comparer);
}
}
}
PickPivotAndPartition
//array partitioning with the quick sort algorithm
private static int PickPivotAndPartition(T[] keys, int lo, int hi, IComparer comparer)
{
int index = lo + (hi - lo) / 2;
ArraySortHelper.SwapIfGreater(keys, comparer, lo, index);
ArraySortHelper.SwapIfGreater(keys, comparer, lo, hi);
ArraySortHelper.SwapIfGreater(keys, comparer, index, hi);
T obj = keys[index];
ArraySortHelper.Swap(keys, index, hi - 1);
int i = lo;
int j = hi - 1;
while (i < j)
{
do
;
while (comparer.Compare(keys[++i], obj) < 0);
do
;
while (comparer.Compare(obj, keys[--j]) < 0);
if (i < j)
ArraySortHelper.Swap(keys, i, j);
else
break;
}
ArraySortHelper.Swap(keys, i, hi - 1);
return i;
}
InsertionSort
//insertion sort
private static void InsertionSort(T[] keys, int lo, int hi, IComparer comparer)
{
for (int index1 = lo; index1 < hi; ++index1) { int index2 = index1; T x; for (x = keys[index1 + 1]; index2 >= lo && comparer.Compare(x, keys[index2]) < 0; --index2)
keys[index2 + 1] = keys[index2];
keys[index2 + 1] = x;
}
}
Now sorting in arrays is represented by a mix of sortings: insertion sort, quicksort, and heapsort.
Usage of Introsort has a positive effect on productivity since data can be partially ordered in real tasks. As we all know, the insertion sort works quite fast with such data.
Productivity Comparison
Comparison with Java
Java drastically differs from .NET in terms of sorting. However, similar to .NET, the Java algorithm has also been changing.
As we know, quicksort is unstable, which is a disadvantage for sorting of referenced types. In Java, this problem doubles. That’s why merge sort is used for sorting linked types. This sorting is stable and ensures execution for O(n logn) of time in the worst case. However, it requires O(n) of additional memory.
Since the stability issue refers only to referenced types, changing elements with one key does not matter for primitive types. That’s why, the improved quicksort algorithm, DualPivotQuicksort, is used for sorting primitive types in Java. Normal Quicksort divides an array into two parts by selecting a random element P. Then, it sorts an array in a way so that all its elements which are less than P are located in the first part, while the rest of elements are located in the second part. DualPivotQuicksort divides an array into three parts instead of two. As a result, the number of moves of array elements drastically decreases.
In Java 7, the sorting algorithm for referenced types has been changed to TimSort.
Timsort is a hybrid stable sorting algorithm, derived from merge sort and insertion sort, designed to perform well on many kinds of real-world data. It was implemented by Tim Peters in 2002. The algorithm finds subsequences of the data that are already ordered and uses that knowledge to sort the remainder more efficiently. This is done by merging an identified subsequence, called a run, with existing runs until certain criteria are fulfilled.
Timesort is fast, but in terms of random data, it loses to the quicksort which is 30-percent faster.
What do you think of this difference of sorting implementation in two frameworks? Do we really need the stability that requires much time (as in Java) and memory for real tasks? Can we prefer speed and memory saving to stability (as in .NET)? Personally, I prefer .NET, since I suppose that stability is required only for certain tasks (I have never used it for last 4 years). Even when stability is highly required, we can put this problem on programmer’s shoulders – I think it is not hard to implement the algorithm of stable sorting.
Conclusion
Perhaps, not every programmer requires so many details on .NET, but still this knowledge never gets in the way. Thank you for reading.
Please feel free to ask any questions and share your thoughts in the comments section.
Tags: .net, c# Last modified: September 23, 2021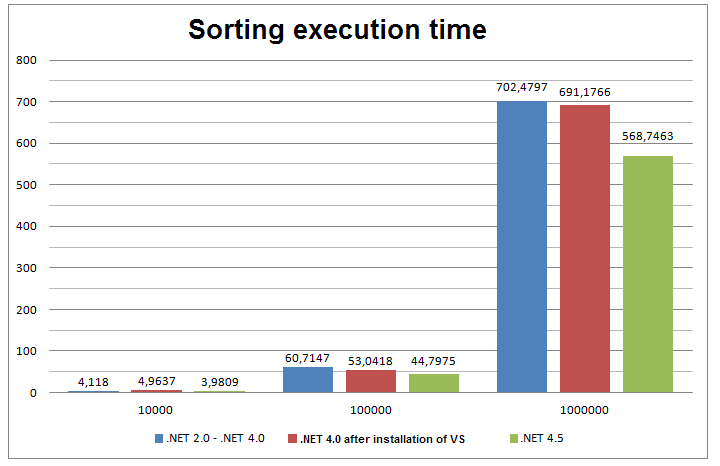






I love these articles! Very interesting insights into the internals of .NET. Keep em coming!
thanks!
I assume you mean caching? 😉
Thanks for your correction. Already fixed that 🙂